密码学简史:从古希腊密报到量子加密的千年博弈
本文基于我此前在公司内部分享的「密码学笔记」打磨而来,现更名为「密码学简史」,更准确地概括了文章的主题与发展脉络。
复杂的事物不存在终极的解决方案,密码学尤其如此。
引言:为什么我们需要加密?
在数字化时代,我们每天都在与密码学打交道:网上银行转账、微信聊天、HTTPS 网站访问…这些看似平常的操作背后,都有着复杂的加密算法在保护我们的隐私和安全。
但密码学的历史远比互联网更加悠久。从古希腊的蜡板密报到现代的量子加密,这是一场跨越数千年的智慧较量,是加密者与破译者之间永无止境的博弈。
密码学发展的时代脉络
密码学的发展可以划分为两个时代,七个世代:
古典加密时代(手工 → 机械电子)
- 隐藏法
- 移位法和替代法
- 维吉尼亚加密法
- 恩尼格玛机
现代加密时代(计算机加密)
- DES 加密系统
- RSA 非对称加密
- 量子加密
这个演进过程的分水岭是计算机的出现,它彻底改变了密码学的游戏规则。
flowchart LR
subgraph 古典加密时代
subgraph 手工加密阶段
A[隐藏法] --> B[移位法和替代法] --> C[维吉尼亚加密法]
end
subgraph 机械电子加密阶段
D[恩尼格玛机]
end
C --> D
end
subgraph 现代加密时代
D --> E[DES加密系统] --> F[RSA加密] --> G[量子加密]
end
第一世代:隐藏法(Steganography)
原理与特点
隐藏法,顾名思义,就是把信息藏起来。这是最原始的信息保护方式,其核心思想是让敌人根本发现不了秘密信息的存在。
破解方法也相对简单:仔细搜寻,这基本上是纯体力活。
历史上的经典案例
🏛️ 拯救古希腊文明的蜡板密报
史上第一个隐藏法的记载来自古希腊历史学家希罗多德。这个故事不仅展现了早期密码学的智慧,更改变了世界历史的走向:
- 当时,强大的波斯帝国计划入侵希腊,斯巴达曾经的老国王的之后,偷偷把这个消息写在木板上又图了一层腊,这片木板成功躲过沿路卫兵检查,到达斯巴达。收信人刮去表面的那层蜡,就发现了下面的密报。得知波斯人的入侵计划后,希腊开始备战。公元前 480 年,波斯舰队以为对方毫无防备,结果一天之内 200 多艘战舰被击沉,五年多的准备毁于一旦。
💡 历史意义:这次密报不仅挽救了雅典和斯巴达,某种程度上也拯救了现代文明。现代文明的两大思想根源——古希腊哲学和后来的基督教思想——得以延续至今。
其他创意隐藏法
古人的想象力在信息隐藏方面展现得淋漓尽致:
- 头皮密信:将送信人的头发剃光,在头皮上写下秘密信息,等头发长出来后派遣出发,到达目的地再剃光头发读取信息
- 体内藏信:将消息写在丝绸上,用蜡包成小球让人吞下,到达目的地后再取出
- 隐形墨水:使用柠檬汁、牛奶等在纸上书写,加热后才能显现文字
现代隐藏法
在数字时代,隐藏法演化为数字隐写术:
- 在图片的像素中隐藏文字信息
- 在音频文件的频谱中嵌入数据
- 利用文本格式(如空格、换行)传递信息
第二世代:移位法和替换法
历史背景
这类加密方法大约在5000 年前就已出现,并统治密码学领域长达 4000 年之久,直到 9 世纪才被阿拉伯数学家发明的频率分析法破解。值得注意的是,欧洲直到 16 世纪才掌握这种破解方法,这从侧面反映了阿拉伯文明在数学和密码学领域的辉煌成就。
移位法(凯撒密码)
移位法是最简单直观的加密方式,其原理是将每个字符在字母表中向前或向后移动固定位数。
📝 实例演示:
1 | 数字示例: |
🔍 在线体验:你可以在 Caesar Cipher Tool 上亲自尝试凯撒密码的加密和解密。
替换法
替换法比移位法更加复杂,它为每个字母指定一个特定的替换字符,而不是简单的位移。
📝 实例演示:
1 | 原文:For man is man and master of his fate |
加密的简单性与解密的复杂性
这些方法的加密过程看起来非常简单,但解密过程却极其困难。这种不对称性正是早期密码学的核心特征。
该方法在人类历史上广泛应用了 4000 多年,期间出现了许多变种:
- 奇偶位变换:奇数位和偶数位使用不同的替换规则
- 字母重排:将奇数位和偶数位的字母分离后重新组合
- 多重替换:对同一文本进行多轮替换加密
破解之道:频率分析法的诞生
暴力破解的困境
想要通过试错法破解替换密码几乎是不可能的:
💭 数学角度思考:假设一条十几个词的消息,每个字母都可能是 26 个字母中的任何一个,那么每增加一个字母,可能的排列方式就增加 26 倍。最终的排列总数可能超过整个宇宙原子的总数,靠碰运气根本无法破解。
频率分析法:概率论的胜利
科学原理
9 世纪的阿拉伯数学家发现了语言的一个重要特征:字母出现的频率并不均等。这一发现彻底改变了密码学的格局。
📊 英文字母频率统计:
- E: 12.7%(最高频)
- T: 9.1%
- A, O, I, N: 6-8%
- Z: 0.1%(最低频)
🔍 在线工具:你可以使用 频率分析工具 来分析任何文本的字母频率。
🌍 多语言适用性
这个规律不仅适用于英语,其他语言也有类似的频率分布特征,这使得频率分析法具有了普遍适用性。
破解步骤
- 收集足够的密文样本:样本越大,统计结果越准确
- 统计字符频率:计算每个密文字符的出现频率
- 频率匹配:将最高频的密文字符对应到语言中最常见的字母(如英文的 E)
- 上下文分析:利用字母组合规律进一步确认
💡 高级技巧:当某些字母频率接近时(如 h=6.09%, r=5.98%, s=6.32%),可以通过分析字母的前后关联来区分。例如:
- t 几乎不会出现在 b, d, g, j, k, m, q 旁边
- h 和 e 经常连在一起
- ee 的出现频率远高于 aa
频率分析法的本质是通过已知的语言统计信息来消除字母排列组合的不确定性。
时间久了,你会发现,工作,其实就是使用已有信息来消除不确定性。
这种解密法出现以后,替代法不再有效,但是加密方不甘失败,很快出现了一种“同音替代法”
比如说字母 a 可以用 11,23,41 三个数字替代,这三个数字翻译过来都是 a。越常用的字母,比如 e,就用越多的符号代替它。这种想法的终极目标,就是让每个数字出现的频率都大致相等。频率特征没有了,密码就不容易破解了。
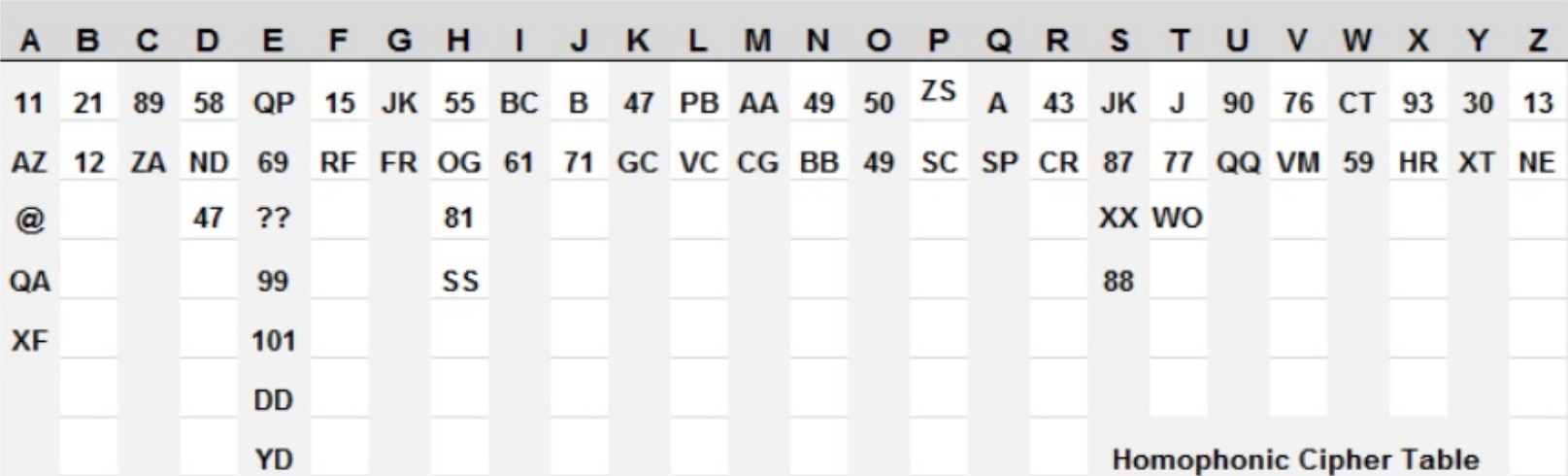
不过这种方法的解密法马上也出现了,就是通过字母前后顺序关系来猜。
最典型的例子是,q 后面出现的最大可能是 u,而 q 又是一个不常用的字母,有很大概率猜出来。其他字母猜出来的难度大一些,但只要肯花时间,总能破解。
第三世代:维吉尼亚加密法 → 产生了“钥匙”的概念
发明人:一般认为是法国外交官:布莱斯·德·维吉尼亚,有争议
凡是出现了一个发明权一堆人抢的情况,就说明那个领域已经形成了成熟的行业。
为了对抗频率分析法,设计了维吉尼亚加密法——“多套符号加密法”。为了掩盖字母使用中的暴露的频率特征,解决办法就是用多套符号代替原来的文字(降频),比如原文中的字母是 A,从前只把它替换成 F,现在把它替换成 F 或者 G 这两个。
那什么时候用 F 什么时候用 G 呢?可以自行规定,比如说,字母在奇数位时用 F 代替,字母在偶数位时用 G 代替。从前单套符号替代的时候,凡是文字中频率为 7.63%的符号,差不多就代表 A 了。但现在 A 由 F 和 G 混合在一起,7.63%的特征不再出现,哪个符号代表 A 就没人知道了,于是频率分析法暂时失效。
扩展的“多套符号加密法”到 26 套字母的方法,就是第三代密码维吉尼亚加密法。
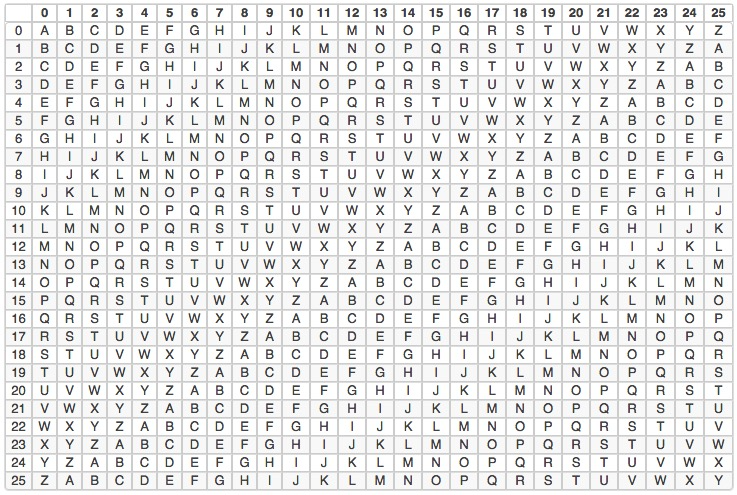
加密过程
假设我要给“hello”加密,现在的思路和单套的加密方法不一样了。单套的时候,我们可以指定这个表里任意一横行,比如指定第 8 行的意思就是说,原文中的字母都往后移 8 位,只使用这一行的规则,“hello”就变成了 PMTTW。
但现在我们的思路是用多套密码,不能只用第 8 行第 8 套。于是我们就这样指定:
原文第一个字母用第 8 套密码代替,第二个字母用第 12 套密码代替,第三个字母用第 5 套密码代替,第四个字母用第 9 套密码代替。
因为这份说明书的文字量比原文还要多得多,而且这个说明书还必须以谁都可以看懂的方式书写。想让收信方看明白,必须要送一本加密说明书给对方,如果说明书被截获,内容也就白加密了。
所以加入了“钥匙”这个概念:
第三代的维吉尼亚加密法在真实使用时,人们事先规定每个字母用了哪套移位法时,并不是毫无规律的瞎指定,而是要约定一个规则,这个规则就叫作 “钥匙”。
钥匙最初只是一个单词,比如,像钥匙是 yes,那怎么加密呢?
你看,yes 的 y 是第 25 个字母,就代表加密时把原文第一个字母往后移 25 位;yes 的第二个字母 e 是字母表中第 5 个字母,就代表把原文的第二个字母往后移 5 位;yes 的第三个字母 s 在字母表中是第 19 个字母,就代表把原文第 3 个字母后移 19 位。这样原文的前三个字母,就分别用了第 25 套、第 5 套、第 19 套替代法。
那原文第 4 个、第 5 个、第 6 个字母怎么解决呢?好办,就按刚刚的规则循环就好。
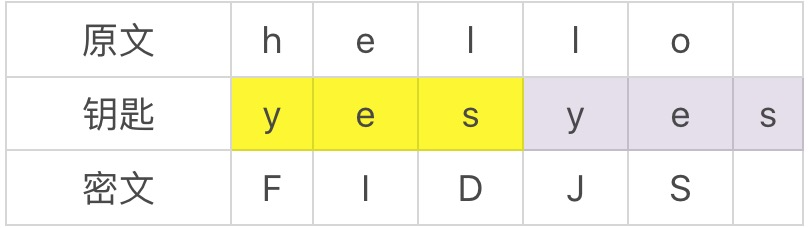
这样“hello”在钥匙是 yes 的情况下,就被加密成了 FIDJS。
这样的好处是,原文里同一个字母会被加密成不同字符,hello 中的两个“l”分别变成了 D 和 J 。而且密文中同样的字符也可能代表不同的原文,谁和谁都不对应。
1586 年,维吉尼亚把这个想法写在了《密码论》中发表。
但这种加密法在发表后的 200 年中,都几乎没有人使用,直到电子和机械时代的来临。
如何破解
“钥匙”是加密解密的核心。
为了处理方便,钥匙最初都是一个正常的单词,比如 dream、flower、king 等,钥匙中每个字母的顺位,表示原文中对应的字母在加密时采用第几套加密法。
原文很长,钥匙很短,为了原文和钥匙一一对应,就反复使用钥匙。例如:key: bed,可以 bedbedbedbed
1 | 原文: the sun and the man in the moon |
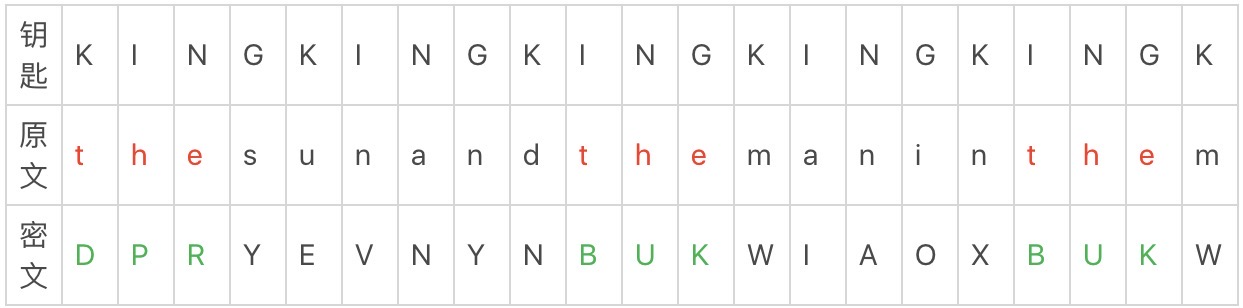
原文的内容中,有 3 个定冠词 the,变成密文后,the 变成了两种样子,第一种是 DPR,第二种是 BUK ,发现BUK 重复了
钥匙是 4 个字母,重复的两个的间距是 8 个字符,正好是钥匙的 2 倍,在钥匙循环到整数倍的时候,如果正好赶上出现了同样的原文,那巧合就出现了,原文就会被加密成相等的密文。
总结破解方法:
第一步,是从密文中找出拼写完全相同的字母串,尤其是那些长度大于 4 的重复出现的密文。比如一篇几百个字母的密文中,长度超过 4,并且重复出现的字母串一共有 4 种,我们就把它们叫作甲乙丙丁。
第二步呢,我们就数一数,它们第一次出现到第二次出现,中间隔了多少个字母。比如说,如果甲字符串重复间隔了 20 个字母,那它代表了什么意义呢?
它就代表这段密文对应的钥匙,在这 20 个字母中,正好反复使用了若干次。那具体是反复使用了 1 次、2 次,还是 4 次呢?其实都有可能。我们把所有可能性都列出来。
比如说间隔 20 个字母后同样的密文再次出现,就有这样几种可能:
- 如果钥匙长度是 2 的话,说明钥匙正好反复使用了 10 次
- 如果钥匙长度是 4 的话,说明钥匙正好使用了 5 次
- 如果钥匙长度是 5 的话,钥匙正好使用了 4 次
- 如果钥匙长度是 10 的话,钥匙正好使用了 2 次
- 如果钥匙长度是 20 的话,钥匙正好使用了 1 次
你发现没有,其实就是把间隔数的所有因数都找出来就对了。这时候乙、丙、丁的情况,也按同样的步骤操作。我们还会得到很多种钥匙长度的可能性。
到底哪个可能性才是对的呢?我们只要看看,哪个因数在所有甲乙丙丁密文的因数列表里都存在,那个因数对应的钥匙长度就是最终的答案。
第四世代:恩尼格玛机(Enigma)——机械加密的巅峰
历史背景
二战密码战
恩尼格玛机是第二次世界大战期间德军使用的机械加密设备,被认为是”不可破解”的密码机器。它的破解直接影响了战争的走向。
图灵的贡献
英国数学家阿兰·图灵领导的团队在布莱切利园成功破解了恩尼格玛密码,这一成就:
- 缩短了二战约 2-4 年
- 拯救了数百万生命
- 奠定了现代计算机科学的基础
技术原理
机械结构
- 转子系统:多个可旋转的编码轮
- 反射器:将信号反射回去
- 插线板:增加额外的替换层
加密过程
- 按下键盘上的字母
- 信号通过插线板进行第一次替换
- 依次通过多个转子进行复杂变换
- 经反射器反射后原路返回
- 最终输出加密字母
安全强度
恩尼格玛机的密钥空间巨大:
- 基础版本:约 10^23 种可能
- 军用版本:超过 10^114 种可能
现代加密时代的开端
第五世代:DES 加密系统
🖥️ 计算机时代的到来
1970 年代,随着计算机的普及,密码学进入了全新的数字时代。美国国家标准局(NBS)发布了数据加密标准(DES)。
🔐 DES 特点:
- 对称加密:加密和解密使用相同密钥
- 分组密码:将数据分成 64 位块进行处理
- 56 位密钥:在当时被认为足够安全
第六世代:RSA 非对称加密——密码学革命
革命性突破
1977 年,Rivest、Shamir 和 Adleman 发明了 RSA 算法,解决了密码学中的一个根本问题:密钥分发问题。
非对称加密原理:
- 公钥:可以公开,用于加密
- 私钥:保密持有,用于解密
- 数学基础:大整数分解的困难性
现代应用:
- HTTPS 网站安全
- 数字签名
- 电子商务
- 区块链技术
第七世代:量子加密——未来的密码学
量子力学原理
量子加密基于量子力学的基本原理:
- 量子不可克隆定理:量子状态无法被完美复制
- 测量扰动:任何窃听行为都会被发现
发展前景:
- 绝对安全:理论上无法被破解
- 量子密钥分发:已有商业化产品
- 量子计算威胁:可能破解现有加密算法
思考与展望
为什么字母语言在加密上更有优势?
📊 统计特征明显
拉丁字母系统具有以下特点:
- 字符集相对较小(26 个字母)
- 频率分布不均匀且稳定
- 组合规律性强
这些特征使得:
- 加密更容易:字符映射关系简单
- 破解更有规律:统计分析方法有效
- 算法设计更成熟:历史积累丰富
汉字系统的挑战
相比之下,汉字系统:
- 字符集庞大(数万个汉字)
- 使用频率分布复杂
- 语义层次多样
这既增加了加密的复杂性,也提供了新的安全可能性。
结语
从古希腊的蜡板密报到量子加密的无限可能,密码学的发展史就是一部人类智慧的进化史。每一次加密技术的突破,都伴随着相应破解方法的出现,这种永恒的攻防博弈推动着密码学不断向前发展。
在数字化时代,密码学已经成为现代社会的基础设施。无论是网上购物、移动支付,还是社交通讯、云计算,都离不开密码学的保护。
未来的挑战与机遇:
- 量子计算的威胁与量子加密的机遇并存
- 人工智能在密码分析中的应用
- 区块链技术带来的新型加密需求
- 隐私保护与监管合规的平衡
💭 思考:在这个信息爆炸的时代,我们每个人都应该了解密码学的基本原理,不仅是为了保护自己的隐私安全,更是为了理解这个数字世界的运行规则。
密码学的故事还在继续,下一个突破性的发明会是什么?让我们拭目以待。
参考资料与延伸阅读
📚 推荐书籍
- 《图解密码技术》(结城浩):图文并茂,入门必读
- 《密码编码学与网络安全》(William Stallings):经典教材,理论与实践并重
- 《应用密码学》(Bruce Schneier):实战导向,附 C 源码
🎬 相关影视作品
- 《模仿游戏》(The Imitation Game) - 本尼迪克特·康伯巴奇主演
- 讲述图灵破解恩尼格玛密码的传奇故事
🎧 音频课程
- 卓克《密码学》30 讲 - 得到 App
- 深入浅出,适合通勤时间学习




