以下仅为学习krahets的 hello-aglo写的笔记

定义

非线性数据结构
表示“祖先”与“后代”的关系
体现分治的思想

class TreeNode{
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode(int x){
        val = x;
    }
}

基础概念回顾

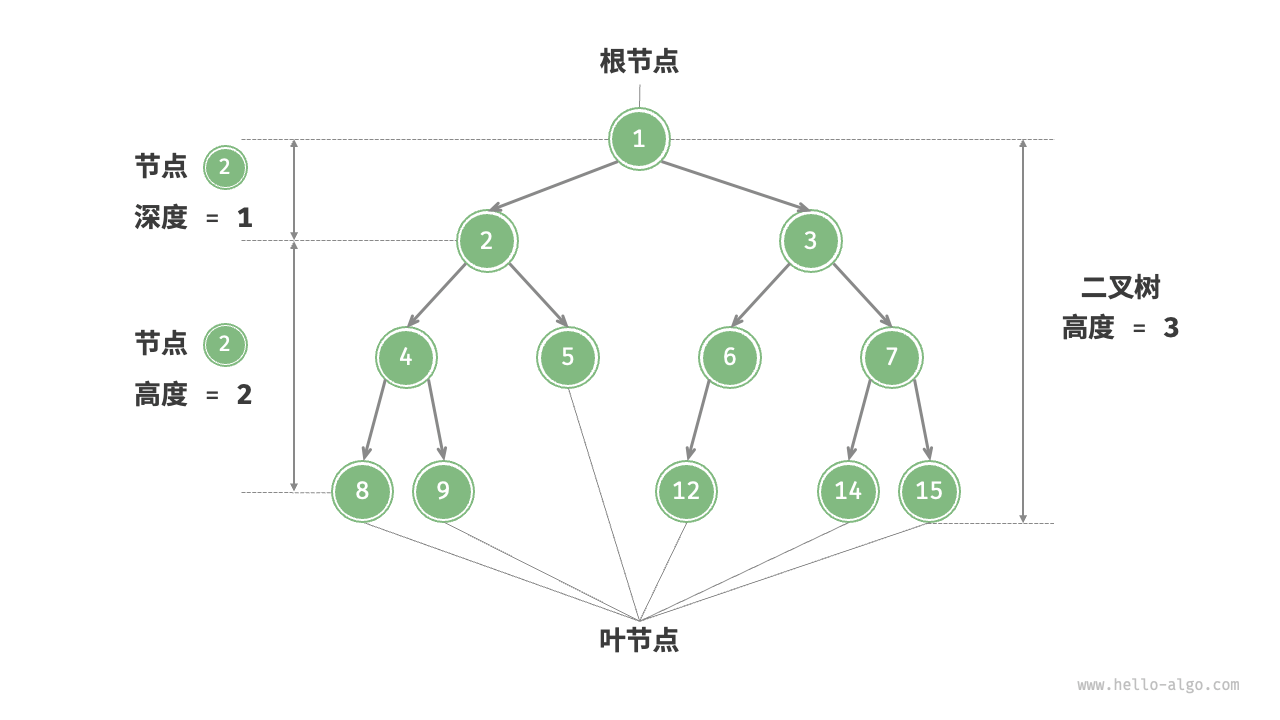
根节点（root）：位于二叉树顶层的节点，没有父节点
叶节点（leaf）：没有子节点的节点，其两个指针指向 None
层（level）：节点所在的层，从顶至底递增，根节点的层是 1
度（degree）：节点所有的子节点数量，二叉树的度是 0、1、2
边（edge）：连接两个节点的线段，即节点的指针引用
节点的深度（depth）：从根节点到该节点所经历的边的数量
二叉树的高度（height）：从根节点到最远叶节点所经历的边的数量
节点的高度（height）：从距离该节点最远的叶节点到该节点所经历的边的数量

图片来自k神的hello-algo项目

二叉树的一般类型

完美二叉树（perfect binary tree)、满二叉树：所有层的二叉树被填满，二叉树达到完美状态，叶节点的度为 0，除叶节点外其他节点的度都为 2
完全二叉树（complete binary tree）：只有最底层的节点未被完全填充，且左右填充节点都靠近左侧
完满二叉树（full binary tree）：除叶节点外，每个节点都有两个节点
平衡二叉树（balanced binary tree）：每一个节点的左子树和右子树高度之差的绝对值不超过 1

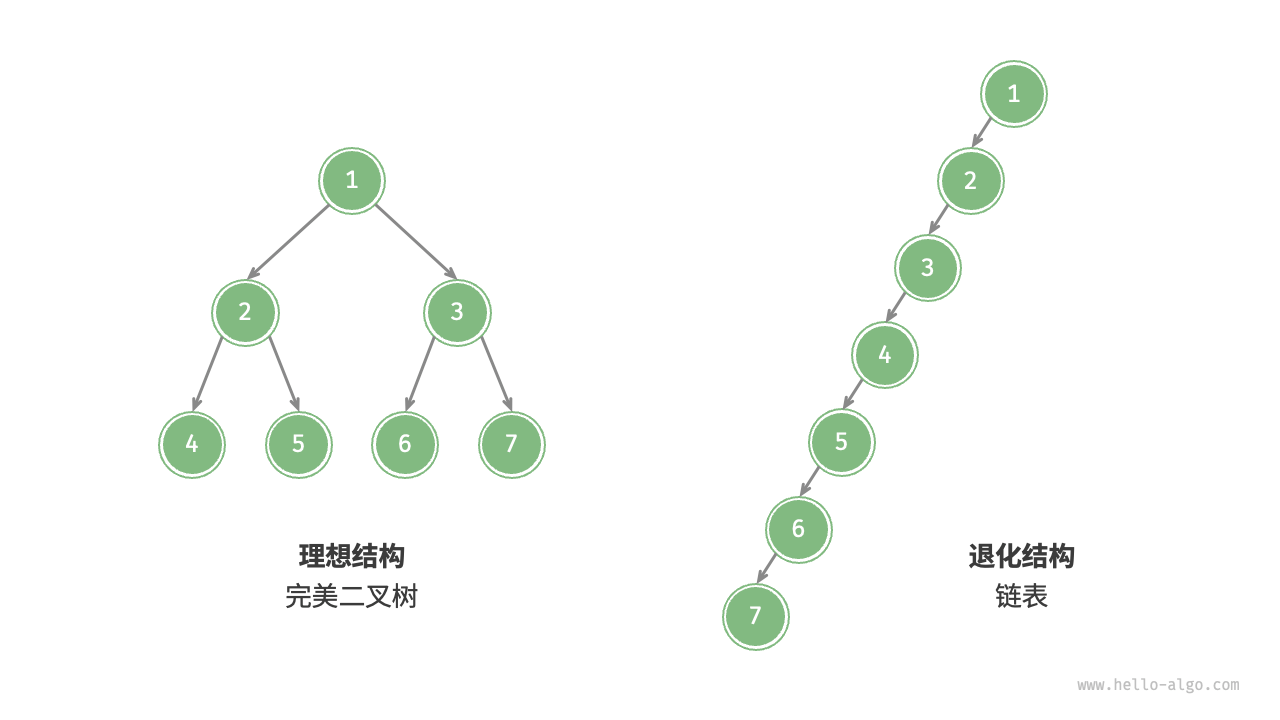
二叉树的退化

二叉树的最佳状态是完美二叉树，充分发挥了分治的思想。
退化的话，会出现只有一边有节点的情况，变成了链表，这时候各项操作都变成线性操作，时间复杂度变成 O(n)了

图片来自k神的hello-algo项目

二叉树的遍历

层序遍历

深度优先

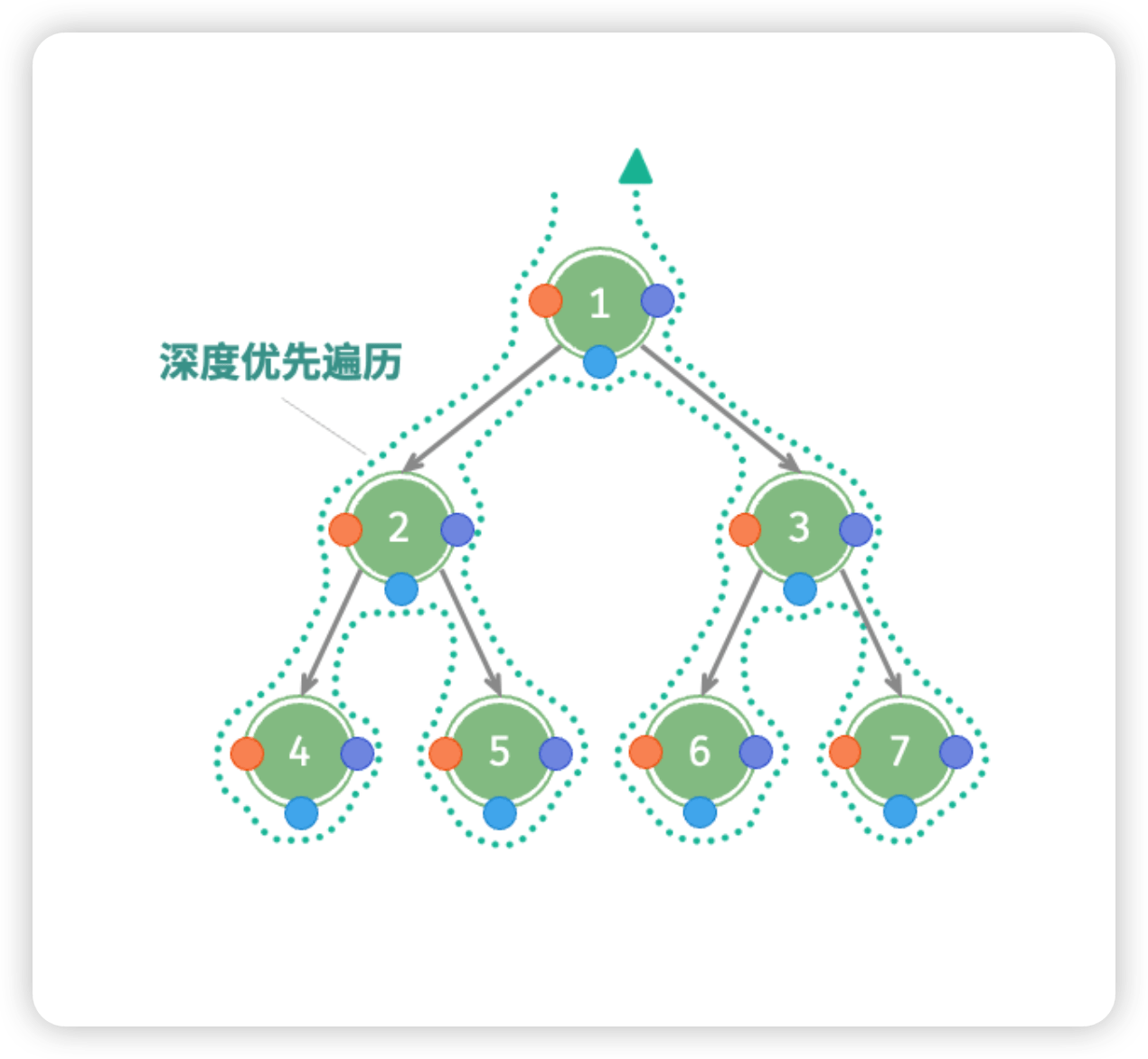
前序遍历

根节点 → 左子树 → 右子树

1 → 2 → 4 → 5 → 3 → 6 → 7

核心算法：

前序遍历(node):
 如果node为空，直接返回(递归终止条件)
 访问node
 前序遍历(node.left)
 前序遍历(node.right)

中序遍历

左子树 → 根节点 → 右子树

4 → 2 → 5 → 1 → 6 → 3 → 7

核心算法：

中序遍历(node):
	如果node为空，直接返回(递归终止条件)
  中序遍历(node.left)
	访问node
  中序遍历(node.right)

后序遍历

左子树 → 右子树 → 根节点

4 → 5 → 2 → 6 → 7 → 3 → 1

核心算法：

后序遍历(node):
	如果node为空，直接返回(递归终止条件)
	后序遍历(node.left)
	后序遍历(node.right)
	访问node

public class BinaryTreeTraversal {
    List<Integer> list = new ArrayList<Integer>(); // 类级变量，用于存储遍历结果

    // 前序遍历
    void preOrder(TreeNode root) {
        if (root == null) {
            return;
        }
        list.add(root.val);
        preOrder(root.left);
        preOrder(root.right);
    }

    // 中序遍历
    void inOrder(TreeNode root) {
        if (root == null) {
            return;
        }
        inOrder(root.left);
        list.add(root.val);
        inOrder(root.right);
    }

    // 后序遍历
    void postOrder(TreeNode root) {
        if (root == null) {
            return;
        }
        postOrder(root.left);
        postOrder(root.right);
        list.add(root.val);
    }

    // 层序遍历
    void levelOrder(TreeNode root) {
        if (root == null) {
            return;
        }
        Queue<TreeNode> queue = new LinkedList<TreeNode>();
        queue.add(root);

        while (!queue.isEmpty()) {
            TreeNode poll = queue.poll();
            list.add(poll.val);
            if (poll.left != null) {
                queue.offer(poll.left);
            }
            if (poll.right != null) {
                queue.offer(poll.right);
            }
        }
    }
}